The basic story here is quite short: in order to have fermions (i.e. quarks) involved in lattice simulations of QCD we need to solve a system of equations. This comes from two things. The first reason is the Grassmann nature of fermions. Therefore we are not able to make computations using Grassmann variables (those are introduced to imply the Pauli exclusion principle). The second reason is a follow up: while using Grassmann algebra and some identities in order to avoid those Grassmann numbers we are ending up with so called pseudo-bosons. So our actual fermions have transformed to bosons, which can be calculated on the computer. Here is where the tricky part comes: along with our transformations we ended up with the inverse of our original matrix. This matrix is quite huge.
A simple calculation involving a rather coarse lattice of 32 sites per spatial and 64 sites in the temporal direction (that is 323 * 64) ends up with a number that is around 1015. Some facts like the precision (relevant for bytes in the machine), complex numbers and others have been omitted for simplification. If we take the resulting 1015 values and print them out on a (gigantic) sheet of paper we could use it to cover Iceland completely.
The problem of huge matrices that have to be inverted or solved in general is not new. Most (physical) simulations have a matrix which has to be solved on one point or the other during execution. This process is usually the biggest time eater for any of those applications. Therefore improving such algorithms is an important task in the mission of faster or more efficient simulations. Actually inventing a new algorithm is quite hard and near to impossible due to the huge research efforts in the last 60 years. Therefore most notable advances are small improvements upon an existing algorithm.
Even though I have some ideas for (completely) new algorithms they are hard to realize and even harder to implement. The process guarantees no success and is quite long which is basically an instant killer. In my Master thesis I focused on an existing algorithm which is combination of FGMRES and GMRES-DR. Both algorithms are build upon the GMRES algorithm which utilizes the Arnoldi iteration in order to build an orthogonalized basis of the newly formed Krylov subspace of the original matrix. This subspace offers some interesting properties which can be used to gather a lot of important information about the matrix.
The work was basically split in 5 parts:
- Exclude GMRES as a basis and try a different one with the very similar FOM algorithm. This part should confirm that FOM could improve the performance of the algorithm for some matrices. This goal was achieved. Unluckily all those matrices are not very important for lattice QCD, leaving us behind with the interesting region being dominated by the superior GMRES algorithm.
- Switch the main solver (not the preconditioner) from single to double precision in order to avoid checks and rounding errors. This should give us a better iteration count while the overall time should increase. The reason for this is increased robustness.
- Use the preconditioner with a slightly different matrix. This should end up with a less precise result from the preconditioner. This should also decrease the time that is used by the preconditioner while not affecting the time of the main solver too much (i.e. overall time should be won here).
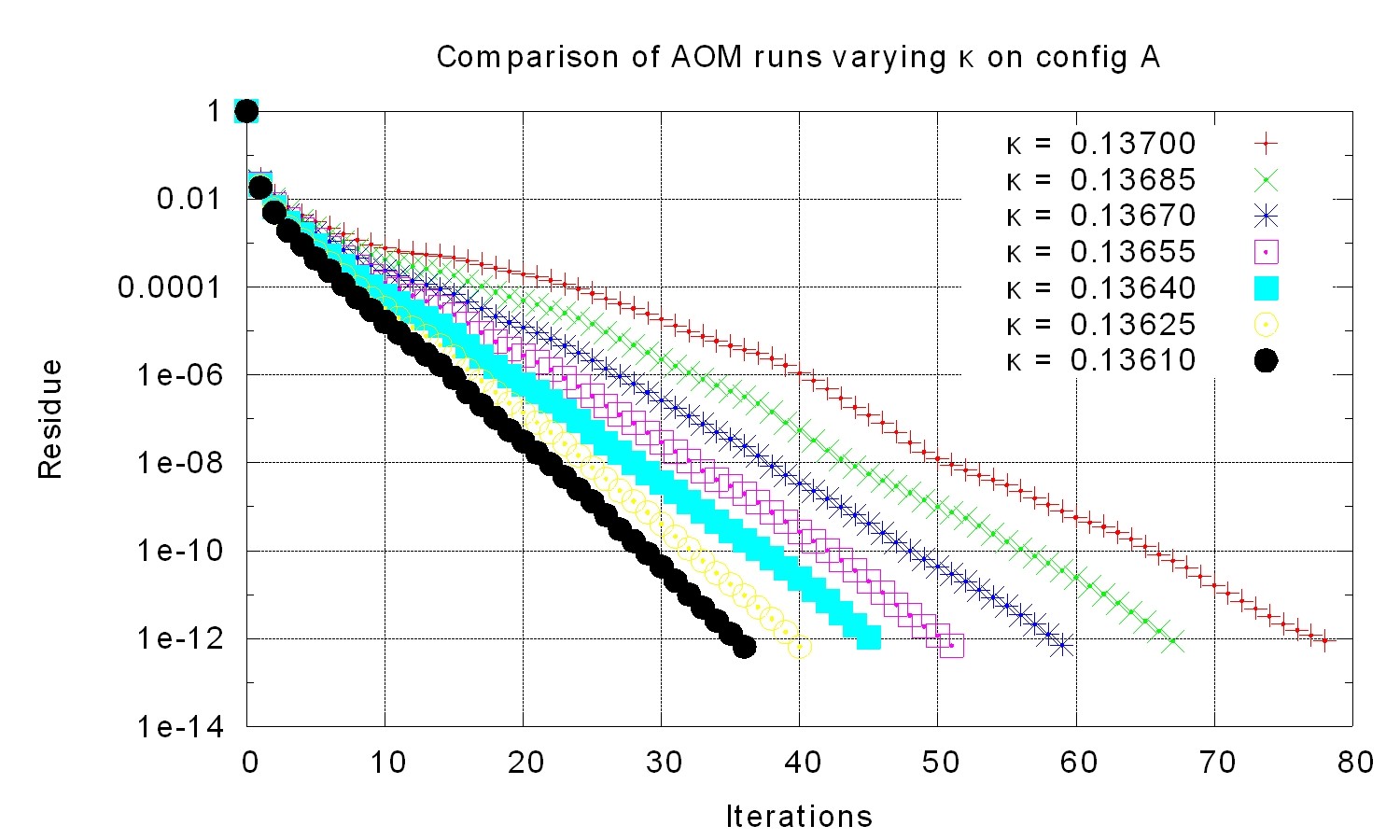
- Implement a new algorithm to get away from static deflation according to some simple formula. The new algorithm should provide a better algorithm by doing dynamic deflation (so called adjusted deflation). This kind of deflation reacts to the precision (convergence) of the eigenvalues and the current slope of the iterative solving process.
- Combine all changes in order to form a new algorithm which takes the best base algorithm (FOM or GMRES) depending on some matrix properties.
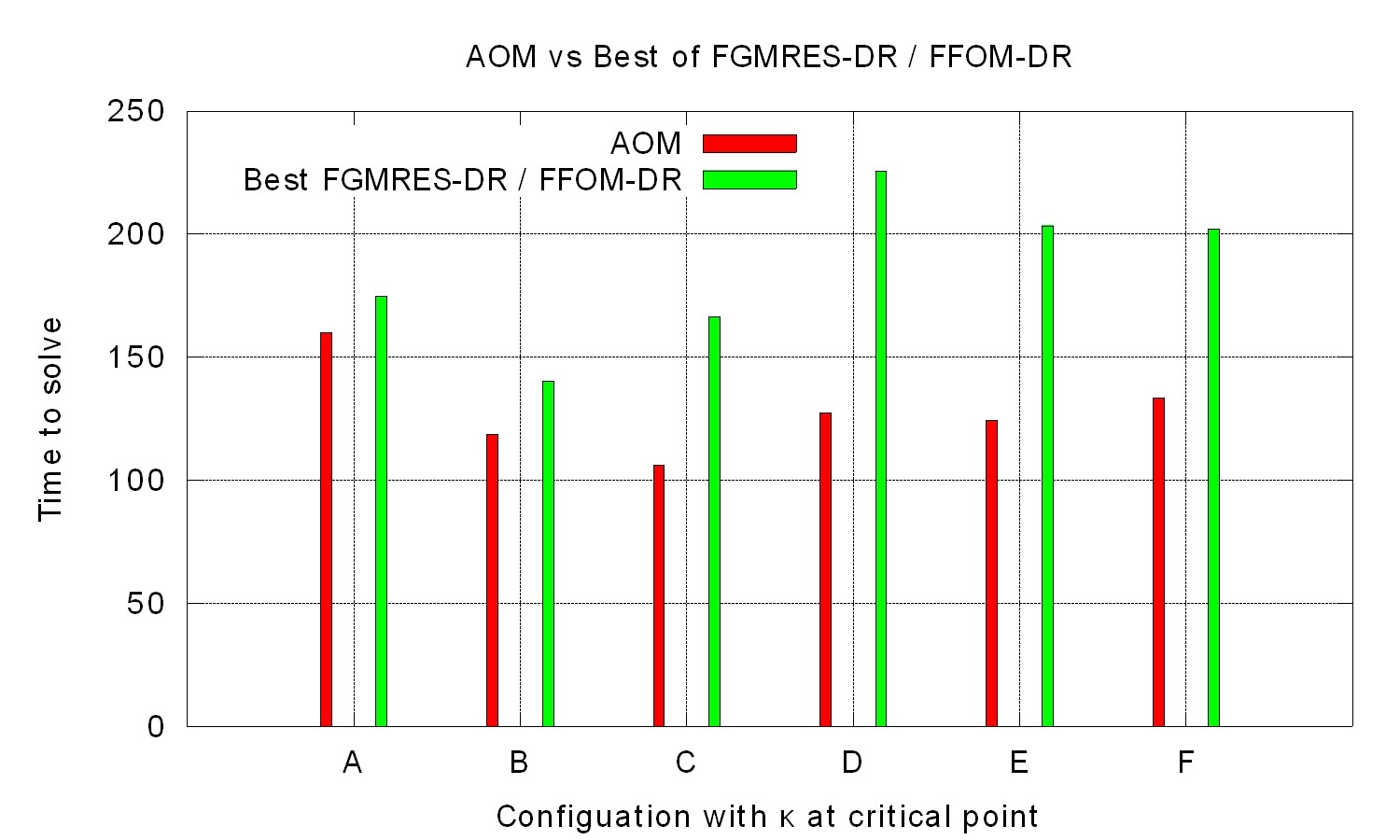
The new algorithm works about 30% faster then the previous one. Therefore the Master thesis was a success.